2024年度の公開模擬テストの受付は2024年3月1日(金)～となります。もうしばらくお待ちください。
偏差値とは
よく偏差値という言葉を耳にします。
一般的に学力測定に使われるもので、偏差値とは、
テストを受けた人たちの中で、自身がどのくらいの位置にいるかを 表す数値
になります。いつも平均点を50に設定し、その人の得点が平均点からどのくらい離れているのかを客観的に計ったものです。自身の得点が平均点と同じなら、偏差値は50になります。また、自身の得点が平均点以上なら偏差値は50以上、平均点よりも下なら偏差値は50未満になります。
なぜ偏差値という考えが必要なのでしょうか？
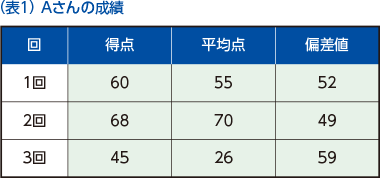
例えば、表1において得点だけを見た場合、2回目が最も成績が良く、3回目には成績が下がってしまったように見えます。平均点を見ればそうではないことがわかりますが、テスト毎に受験者1人ひとりの得点や平均点も変化するため、自身の得点と平均点の差だけでは正確な位置を知ることはできません。そのために、自身がどのくらいの位置にいるかシンプルに数値化された偏差値は、受験勉強において非常に有効な評価方法だと言えます。
偏差値の算出には平均点が必要です。そして、この平均点が正確であればあるほど、つまり、受験者数が多ければ多いほど、算出される偏差値も正確になります。
偏差値のメリット・デメリット
偏差値のメリットは、
◆客観的に集団内の自身の学力を計ることができる点
◆得意教科や苦手教科の把握が容易な点
にあります。
先ほども述べましたが、テスト毎に平均点は変化します。テストの難易度や受験した人たちの学力層など、要因は様々です。そのため、集団内の学力を計るには、自身の得点や平均点だけではなく、偏差値を用いるのが有効です。
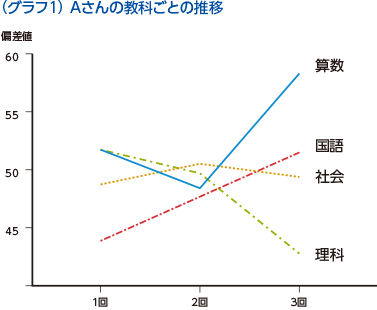
また、偏差値を使って、苦手な教科を割り出すこともできます。単純に、他の教科と比較して、偏差値の低い教科が苦手な教科であると言えます。グラフ1のように、教科ごとに偏差値の推移を考慮して、自分にはどの教科の勉強が不足しているのかを的確にとらえることができれば、成績向上のための対策をとることができます。
一方、偏差値のデメリットは、
母集団（テストを受験した人たち）が変わると、比較することができない点
にあります。例えば、同じ時期に学校内のテスト・三重県内のテスト・全国規模のテストを受けたとします。これらは全て母集団が異なるため、偏差値を用いて結果の比較が行えません。学校のテストや全国規模のテストで自身の位置が計れても、原則、三重県内の人たちだけが受ける三重県立高校入試では、そのデータを用いることができません。
ですから、入試のためには、
◆受験者数ができるだけ多いテスト
◆母集団が本番の入試に できるだけ近いテスト
この2点をふまえて、テスト選びをする必要があります。
来る入試に向けて、最短距離で学力を向上させるためにも、早い段階から「同じ学校を目指す人たち」の中での相対的な自身の位置を把握することができるeisuの公開模擬テストをぜひご活用ください。
